leetcode-51. N 皇后

JAVA解法

class Solution {
    public List<List<String>> solveNQueens(int n) {
        // 定义变量储存结果集
        List<List<String>> solutions = new ArrayList<List<String>>();
        // 定义跟传入的皇后个数一样多的整形数组
        int[] queens = new int[n];
        // 对数组全赋值为 -1
        Arrays.fill(queens, -1);
        // 定义三个集合分别记录每一列以及两个方向的每条斜线上是否有皇后
        Set<Integer> columns = new HashSet<Integer>();
        Set<Integer> diagonals1 = new HashSet<Integer>();
        Set<Integer> diagonals2 = new HashSet<Integer>();
        // 进行回溯
        backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
        // 返回最终结果
        return solutions;
    }

    // 回溯的实现
    public void backtrack(List<List<String>> solutions, int[] queens, int n, int row, Set<Integer> columns, Set<Integer> diagonals1, Set<Integer> diagonals2) {
        // 当皇后个数跟行数一样的时候证明符合条件且经排列完成
        if (row == n) {
            // 生成符合要求的棋盘布局
            List<String> board = generateBoard(queens, n);
            // 将本次解法加入结果集数组中
            solutions.add(board);
        } else {
            // 否则，判断哪一行那一列符合要求能放入皇后
            for (int i = 0; i < n; i++) {
                // 如果该列已经有了皇后则进行下一个 for 循环
                if (columns.contains(i)) {
                    continue;
                }
                // 如果还没有皇后，则判断斜线上是否有皇后
                int diagonal1 = row - i;
                // 如果该斜线上已经有了皇后则进行下一个 for 循环
                if (diagonals1.contains(diagonal1)) {
                    continue;
                }
                // 如果还没有皇后，则判断另一个斜线上是否有皇后
                int diagonal2 = row + i;
                // 如果该斜线上已经有了皇后则进行下一个 for 循环
                if (diagonals2.contains(diagonal2)) {
                    continue;
                }
                // 如果没有皇后，则确定这个位置符合放置皇后，将此时的行数作为数组的下标，列数作为该数组的对应行坐标的值存进去，记录入当前选择的位置
                queens[row] = i;
                // 记录入受影响的列和两个斜线
                columns.add(i);
                diagonals1.add(diagonal1);
                diagonals2.add(diagonal2);
                // 递归主体
                backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
                // 还原当前选择的位置
                queens[row] = -1;
                columns.remove(i);
                // 还原受影响的列和两个斜线，让下一次通过层次的选择不受影响
                diagonals1.remove(diagonal1);
                diagonals2.remove(diagonal2);
            }
        }
    }

    // 生成结果棋盘的方法
    public List<String> generateBoard(int[] queens, int n) {
        // 定义存储棋盘的结果集
        List<String> board = new ArrayList<String>();
        // 生成棋盘的核心方法
        for (int i = 0; i < n; i++) {
            // 定义一个长度为皇后个数的 char 数组
            char[] row = new char[n];
            // 将其全部填充 '.'
            Arrays.fill(row, '.');
            // 再将上边记录皇后可以放的位置的对应地方用 'Q' 覆盖 '.'
            row[queens[i]] = 'Q';
            // 将 char 类型的数组转换为 String 类型添加到结果集中
            board.add(new String(row));
        }
        // 返回存储棋盘的结果集
        return board;
    }
}

题解分析

  这道题用基于集合的回溯的方法。在主体方法中，先定义变量储存最终结果集的变量，定义跟传入的皇后个数一样多的整形数组来储存皇后摆放的位置，对数组全赋值为 -1 也就是一个初始化的操作，定义三个集合分别记录每一列以及两个方向的每条斜线上是否有皇后，进行回溯，最终完回溯后返回最终结果集即可。
  进入回溯算法之前对皇后个数与当前行数进行判断，当皇后个数跟行数一样的时候证明符合条件且经排列完成，则需要生成符合要求的棋盘布局，并将本次解法加入结果集数组中，也就是本次成功的布局；当皇后个数跟行数不一样的时候证明排列还在进行中，则需要判断哪一行那一列符合要求能放入皇后，先判断该列，如果该列已经有了皇后则进行下一个 for 循环。如果该列没有，则判断两个方向的斜线是否有皇后，如果任一斜线上已经有了皇后则进行下一个 for 循环，如果没有皇后，则确定这个位置符合放置皇后，将此时的行数作为数组的下标，列数作为该数组的对应行坐标的值存进去，记录入当前选择的位置和受影响的列和两个斜线。接着进入下一个递归，列数不变但是行数加一，其它参数一样。记得还原当前选择的位置，还原受影响的列和两个斜线，让下一次通过层次的选择不受影响，这是回溯的特性。
  上文提到的生成结果棋盘的方法是先定义存储棋盘的结果集，用 for 循环生成 n 行 n 列的棋盘，n 为皇后个数。在 for 循环中定义一个长度为皇后个数的 char 数组，将其全部填充 ‘.’，再将上边记录皇后可以放的位置的对应地方用 ‘Q’ 覆盖 ‘.’，将 char 类型的数组转换为 String 类型添加到结果集中，并返回存储棋盘的结果集即可完成棋盘制作。
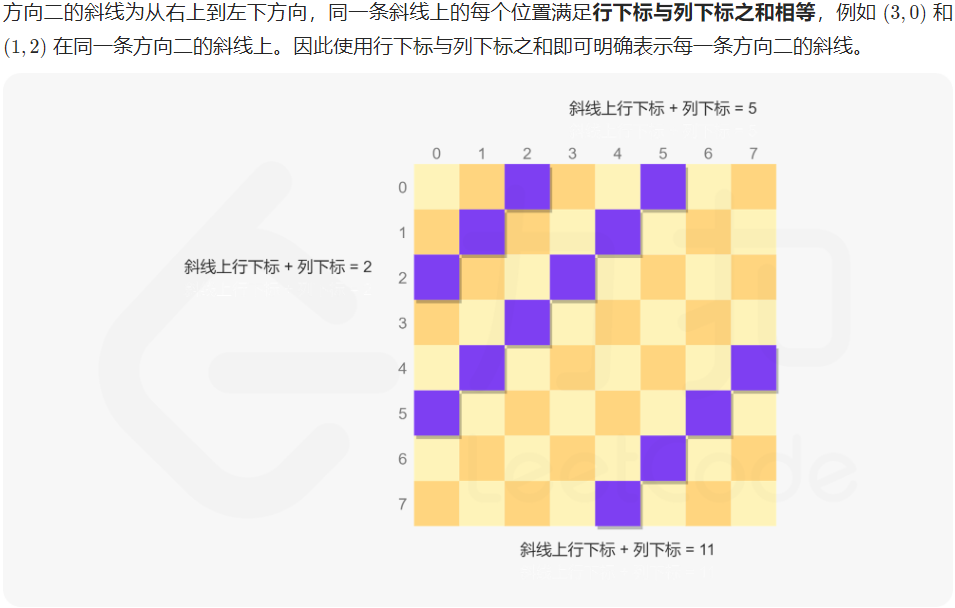
  以上提到的两个方向的斜线的定义如下：


leetcode原题：51. N 皇后